GDLSのAI活用

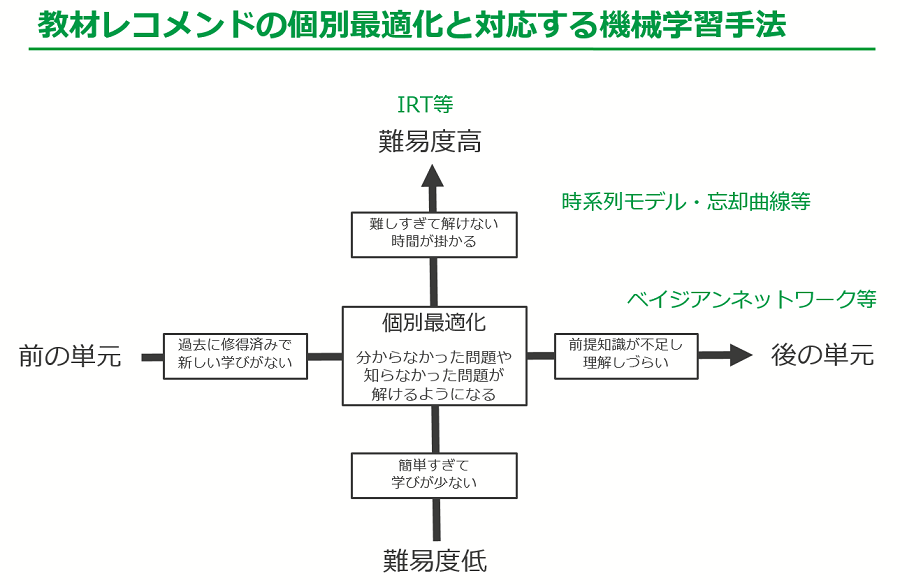
生徒一人一人の学習履歴に基づき、最適な単元かつ難易度の教材を必要なタイミングでレコメンドし、効率良く学習する事を目指しています。
まず、最適な難易度の教材についてIRTにより、いわゆる視力検査で一部の輪のみを見るだけで視力が測れる事と同様なアプローチで、少ない問題数で精度高く理解度や難易度の判定が可能となります。
また、実施数が少ない単元もベイジアンネットにより、関連する単元の理解度の状況からある程度推定する事で必要な単元に絞る事ができ、効果的な学習が行えます。
さらに、一度学習したとしても忘却曲線や時系列モデルに基づき、必要な教材を再度実施させて定着促進を行う事で、忘れすぎる事による再習得にかかる無駄を削減しております。

IRT

IRT（Item Response Theory）は、教育評価や心理測定などの領域で使用される統計的なモデルです。IRTは、受検者の能力とテストアイテムの特性の関係性をモデル化することに焦点を当てています。

IRTは、テストアイテム（質問や問題）と受検者の能力との関係を確率的にモデル化します。各アイテムは、受検者の能力に応じて正しい回答をする確率を持ちます。IRTでは、アイテムの特性パラメータとして、以下の3つの主要なパラメータが使用されます。

困難度（Difficulty）: アイテムの困難度は、能力が平均的な受検者が正答する確率を表します。困難度が高いアイテムは、高い能力を持つ受検者が正答する確率が高くなります。

識別度（Discrimination）: アイテムの識別度は、能力の高い受検者と低い受検者の間で、アイテムに正答する確率の差を表します。識別度が高いアイテムは、能力の高い受検者と低い受検者の間で明確に区別できるようなアイテムです。

推測度（Guessing）: アイテムの推測度は、受検者が無知のままでアイテムに正答する確率を表します。推測度が低い場合、受検者が無知のままでアイテムに正答する確率は低くなります。

IRTは、これらのアイテム特性パラメータと受検者の能力を組み合わせて、受検者の能力を推定することができます。IRTモデルは、一般的に、1パラメータモデル（1PL）、2パラメータモデル（2PL）、および3パラメータモデル（3PL）のように、異なるパラメータの組み合わせで表現されます。

IRTの利点は、テストの信頼性と妥当性を向上させることです。IRTは、テストのアイテムを選択するための効果的な方法や、テストスコアの比較や受検者の能力の推定に基づく意思決定を支援するためのフレームワークとして広く使用されています。

GDLSで提供している多変量IRT（Multidimensional Item Response Theory）は、IRTの拡張形であり、複数の能力次元を考慮したアイテム反応モデリングの手法です。通常のIRTでは、受検者の能力を単一の次元でモデル化しますが、多変量IRTでは、受検者の能力が複数の相互関連する次元で表されることを考慮します。

多変量IRTは、教育評価、心理測定、人格評価など、さまざまな領域で使用されています。能力の複数次元を考慮することで、より精緻な情報と洞察を提供し、適切な意思決定や介入の基盤となります。

ベイジアンネットワーク

ベイジアンネットワーク（Bayesian Network）は、確率的なモデリング手法の一種です。ベイジアンネットワークは、複数の変数間の因果関係を表現し、変数間の依存関係や不確実性を表すために使用されます。

ベイジアンネットワークは、有向非巡回グラフ（Directed Acyclic Graph, DAG）として表現されます。ノードは変数を表し、エッジは変数間の因果関係を示します。エッジがある場合、その先のノードは原因となる変数に依存しています。このような因果関係は条件付き確率を使ってモデル化され、ノード間の依存関係を表現します。

各ノードは条件付き確率表（Conditional Probability Table, CPT）と呼ばれる表で表現されます。CPTは、そのノードの親ノードの値に基づいて、そのノードの確率分布を示します。これにより、ノード間の依存関係や条件付き確率を明示的にモデル化することができます。

ベイジアンネットワークは、以下のような様々なタスクに適用されます。

推論（Inference）: 与えられた観測データから、未知の変数の値を推定します。ベイジアンネットワークは、条件付き確率を利用して、未知の変数の事後分布を計算することができます。

モデリング（Modeling）: ベイジアンネットワークは、現象やシステムのモデル化に使用されます。変数間の因果関係を明示的に表現することで、問題領域の理解を深めることができます。

データマイニング（Data Mining）: ベイジアンネットワークは、大量のデータからパターンや関係性を抽出するために使用されます。データの分布や依存関係を考慮して、データの予測や分類を行うことができます。

ベイジアンネットワークは、医療診断、リスク評価、画像処理、自然言語処理など、さまざまな分野で応用されています。因果関係のモデリングと不確実性の取り扱いが必要な場面で、ベイジアンネットワークは有用なツールとなります。

ベイジアングラフィカルネットワーク（Bayesian Graphical Network）は、ベイジアンネットワーク（Bayesian Network）の一種です。ベイジアングラフィカルネットワークは、確率的なモデリングや因果関係の可視化に使用されます。

時系列モデル

時系列モデルは、時間的な順序で観測されるデータのパターンや振る舞いを分析するための統計モデルです。時系列データは、連続的な時間間隔で観測されるデータの系列であり、例えば株価、気温、売上データなどが該当します。

時系列モデルの目的は、過去のデータのパターンやトレンドを分析し、将来の値を予測することです。時系列データは通常、以下のような特性を持っています。

トレンド（Trend）: データが長期的に増加または減少している傾向を示すパターン。

季節性（Seasonality）: データに周期的なパターンがあり、特定の季節や時間帯での規則的な変動が見られるパターン。

サイクル（Cycle）: データに長期的な周期性があり、季節性よりも長いスパンでの変動が見られるパターン。

ノイズ（Noise）: データにランダムな変動や誤差が存在する要素。

時系列モデルは、これらの特性を捉えるために様々な手法やモデルが使用されます。代表的な時系列モデルには以下のものがあります。

自己回帰モデル（Autoregressive Models）: 過去のデータの線形結合に基づいて未来の値を予測するモデル。AR(p)モデルやARIMAモデルがあります。

移動平均モデル（Moving Average Models）: 過去の誤差項の線形結合に基づいて未来の値を予測するモデル。MA(q)モデルやARIMAモデルに組み込まれることもあります。

自己回帰移動平均モデル（Autoregressive Moving Average Models）: 自己回帰モデルと移動平均モデルを組み合わせたモデル。ARMA(p,q)モデルやARIMAモデルがあります。

季節性モデル（Seasonal Models）: 季節性を考慮したモデル。季節自己回帰移動平均モデル（SARIMA）や季節性指数モデル（Seasonal Exponential Smoothing）があります。

状態空間モデル（State Space Models）: 潜在的な状態変数と観測値の関係を表現するモデル。カルマンフィルタやカルマンスムーザなどが使用されます。

これらのモデルを使用して、過去のデータを解析し、将来の値の予測や変動の解釈を行うことができます。時系列モデルは、経済予測、天気予報、在庫管理、需要予測など、さまざまな分野で活用されています。